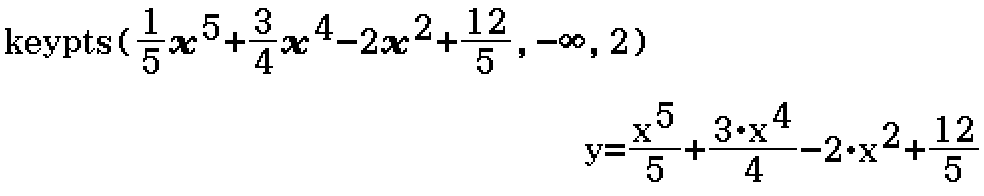keypts (Program)
Command last updated 9/7/2022.
Download
IMPORTANT - requires printpts stored in the same folder as your current folder or in the “library” folder (see the Variable Manager).
keypts(f, l, u)
- f is an expression in terms of x (execution of Program may partially fail if there are other unknown variables in the expression)
- l is the lower boundary of x (l should not be in terms of unknown variables)
- u is the upper boundary of x (u should not be in terms of unknown variables)
Prints and categorises coordinates of key points on y=f in the domain xϵ[l, u].
- y-axis intercepts where x=0
- x-axis intercepts where y=0
- stationary points where f \('\)=0
- local minima where f \(''\)>0
- local maxima where f \(''\)<0
- stationary points of inflection where f \(''\)=0 and f \('''\)≠0
- stationary points of unknown nature where f \(''\)=0 and f \('''\)=0 (users should verify the nature of these points themselves)
- points of inflection where f \(''\)=0 and f \('''\)≠0
- possible points of inflection where f \(''\)=0 and f \('''\)=0 (users should verify the nature of these points themselves)
- endpoints where x=l and x=u
The 2nd and 3rd derivative tests are not on the VCE Mathematical Methods Study Design.
Example
Find key points on \(y = \dfrac{1}{5} x^5 + \dfrac{3}{4} x^4 - 2x^2 + \dfrac{12}{5}\) for \(x \in (-\infty, 2]\).