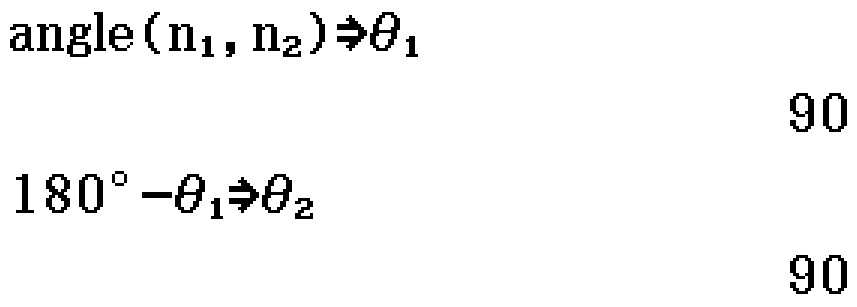3D-Planes (eActivity)
Command last updated 6/3/2024.
Download
Extends Charlie Watson’s eActivity. Modify the values of the input variables, then click the top line and hit EXE. The outputs are stored in the relevant variables.
Plane 3 pts
Find vector and Cartesian equations of plane given 1 point and 2 direction vectors on plane.
Input: A, B, C
- A, B, C are point vectors on plane
Output: A, AB, AC soln, n, q, E
- A is point vector on plane
- AB, AC are direction vectors on plane
- WARNING: If soln has 2 or more of x=x, y=y or z=z then ABC are collinear and infinite number of normals exist
- n is normal vector
- q is number
- E is Cartesian equation
r = A + λAB + μAC
r·n = q (n = ai + bj + ck)
ax + by + cz = q
Example
Find a Cartesian equation of the plane containing points \((1, 0, 2)\), \((2, 3, 0)\) and \((1, 2, 1)\). (Sample Specialist Exam 2 Section B Question 5aii)
![A = [1, 0, 2]; B = [2, 3, 0]; C = [1, 2, 1]](/files/3D-PlanesPlane3pts0.png)
![A = [1, 0, 2]; AB = [1, 3, -2]; AC = [0, 2, -1]; soln = {x=z/2, y=z/2, z=z}; n = [1/2, 1/2, 1]; q = 5/2; E = x/2+y/2+z=5/2](/files/3D-PlanesPlane3pts1.png)
Plane 1 pt, 2 vectors
Find Cartesian equation of plane given 1 point and 2 direction vectors on plane.
Input: A, P, Q
- A is point vector on line
- P, Q are direction vectors on plane
Output: soln, n, q, E
- WARNING: If soln has 2 or more of x=x, y=y or z=z then P and Q are parallel vectors and infinite number of normals exist
- n is normal vector
- q is number
- E is Cartesian equation
r = A + λP + μQ
r·n = q (n = ai + bj + ck)
ax + by + cz = q
Example
Find a Cartesian equation of the plane described by \(x = 1 + 2s + 3t\), \(y = -2 - s - 2t\) and \(z = 2 - s + t\). (Sample Specialist Exam 2 Section B Question 3b)
![A = [1, -2, 2]; P = [2, -1, -1]; Q = [3, -2, 1]](/files/3D-PlanesPlane1pt2vectors0.png)
![soln = {x=x, y=5x/3, z=x/3}; n = [1, 5/3, 1/3]; q = -5/3; E = x + 5y/3 + z/3 = -5/3](/files/3D-PlanesPlane1pt2vectors1.png)
Plane Cartesian
Find vector equation of plane given Cartesian equation of plane.
Input: n, q
- n is normal vector to plane
- q is number
Output: A, P, Q
- A is point vector on plane
- P, Q are direction vectors on plane
ax + by + cz = q
r·n = q (n = ai + bj + ck)
r = A + λP + μQ
Example
Find a vector equation of the plane \(2x + 3y - 5z = 7\).
![n = [2, 3, -5]; q = 7](/files/3D-PlanesPlaneCartesian0.png)
![A = [7/2, 0, 0]; P = [5/2, 0, 1]; Q = [-3/2, 1, 0]](/files/3D-PlanesPlaneCartesian1.png)
Intersection plane-line
Find intersection between line and plane.
Input: a, b, n, p
- a is point vector on line
- b is direction vector along line
- n is normal vector to plane
- p is point vector on plane
Output: X
- X is point vector of intersection
r = a + tb
r·n = p·n
Example
Find the point of intersection between the plane \(2x - 2y - z = -18\), and a line normal to the plane passing through the origin. (2023 Specialist Exam 2 Section B Question 5f)
![a = [0, 0, 0]; b = [2, -2, -1]; n = [2, -2, -1]; p = [0, 0, 18]](/files/3D-PlanesIntersectionplaneline0.png)
![X = [-4, 4, 2]](/files/3D-PlanesIntersectionplaneline1.png)
Intersection plane-plane
Find intersection between two planes.
Input: P1, n1, P2, n2
- P1 is point vector on plane 1
- n1 is normal vector to plane 1
- P2 is point vector on plane 2
- n2 is normal vector to plane 2
Output: A, B
- A is point vector on intersection line
- B is direction vector along intersection line
r·n1 = P1·n1
r·n2 = P2·n2
r = A + λB
Example
Find the line of intersection between the planes \(x + y + 2z = 5\) and \(x - y - z = 0\). (Sample Specialist Exam 2 Section B Question 5bii)
![P1 = [5, 0, 0]; n1 = [1, 1, 2]; P2 = [0, 0, 0]; n2 = [1, -1, -1]](/files/3D-PlanesIntersectionplaneplane0.png)
![A = [0, -5, 5]; B = [1, 3, -2]](/files/3D-PlanesIntersectionplaneplane1.png)
Distance plane-point
Find shortest distance between point and plane.
Input: A, P, n
- A is point vector of point
- P is point vector on plane
- n is normal vector to plane
Output: D
- D is shortest distance
r·n = P·n
Example
Find the shortest distance between the origin and the plane \(2x - 2y - z = -18\). (2023 Specialist Exam 2 Section B Question 5e)
![A = [0, 0, 0]; P = [0, 0, 18]; n = [2, -2, -1]](/files/3D-PlanesDistanceplanepoint0.png)
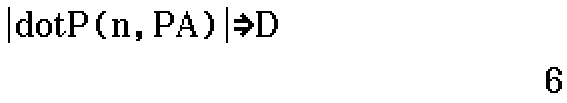
Distance plane-line
Find shortest distance between line and plane.
Input: A, B, P, n
- A is point vector on line
- B is direction vector along line
- P is point vector on plane
- n is normal vector to plane
Output: D
- D is shortest distance
r = A + λB
r·n = P·n
Example
Find the shortest distance between the line \(\mathbf{r}(t) = \mathbf{i} + \mathbf{j} - 5\mathbf{k} + t(4\mathbf{i} + 2\mathbf{j} + 2\mathbf{k})\) and the plane \(2x - 3y - z = 2\). (Sample Specialist Exam 2 Section B Question 4c)
![A = [1, 1, -5]; B = [4, 2, 2]; P = [1, 0, 0]; n = [2, -3, -1]](/files/3D-PlanesDistanceplaneline0.png)

Distance plane-plane
Find shortest distance between two planes.
Input: P1, n1, P2, n2
- P1 is point vector on plane 1
- n1 is normal vector to plane 1
- P2 is point vector on plane 2
- n2 is normal vector to plane 2
Output: D
- D is shortest distance
r·n1 = P1·n1
r·n2 = P2·n2
Example
Find the shortest distance between the planes \(5x - 4y - 12z = 10\) and \(-15x + 12y + 36z = 20\). (Sample Specialist Exam 2 Section A Question 6)
![P1 = [2, 0, 0]; n1 = [5, -4, -12]; P2 = [0, 5/3, 0]; n2 = [-15, 12, 36]](/files/3D-PlanesDistanceplaneplane0.png)
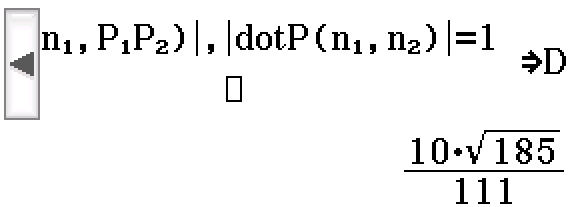
Angle plane-line
Find both angles between line and plane.
Input: b, n
- b is direction vector along line
- n is normal vector to plane
Output: θ1, θ2
- θ1, θ2 are angles
r = a + λb
r·n = k
Example
Find the acute angle at which the line \(\mathbf{r}(t) = 3\mathbf{i} + 2\mathbf{j} + 4\mathbf{k} + t(\mathbf{i} - 2\mathbf{j} + 2\mathbf{k})\) intersects the plane \(2x - 2y - z = -18\). (2023 Specialist Exam 2 Section B Question 5c)
![b = [1, -2, 2]; n = [2, -2, -1]](/files/3D-PlanesAngleplaneline0.png)
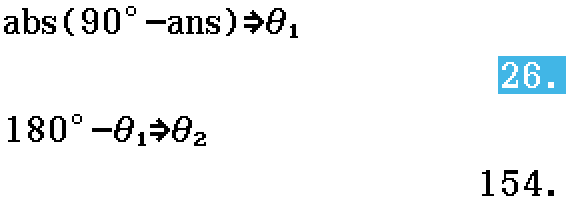
Angle plane-plane
Find both angles between two planes.
Input: n1, n2
- n1 is normal vector to plane 1
- n2 is normal vector to plane 2
Output: θ1, θ2
- θ1, θ2 are angles
r·n1 = k1
r·n2 = k2
Example
Find the value of \(k\) for which the planes \(2x - ky + 3z = 1\) and \(2kx + 3y - 2z = 4\) are perpendicular. (2023 Specialist Exam 2 Section A Question 18)
![n1 = [2, -6, 3]; n2 = [2*6, 3, -2]](/files/3D-PlanesAngleplaneplane0.png)