3D-Lines (eActivity)
Command last updated 6/3/2024.
Download
Extends Charlie Watson’s eActivity. Modify the values of the input variables, then click the top line and hit EXE. The outputs are stored in the relevant variables.
Line 2 pts
Find vector and Cartesian equations of line given 2 points on line.
Input: A, B
- A, B are point vectors on line
Output: A, AB, C
- A is point vector on line
- AB is direction vector along line
- C is list representing Cartesian equation
C = {(x-a)/b, (y-c)/d, (z-e)/f} represents (x-a)/b = (y-c)/d = (z-e)/f
r = A + λAB
Example
Find the line passing through points \((-3, -1, -10)\) and \((5, -6, 4)\). (Sample Specialist Exam 2 Section A Question 4)
![A = [-3, -1, -10]; B = [5, -6, 4]](/files/3D-LinesLine2pts0.png)
![A = [-3, -1, -10]; AB = [5, -6, 4]; C = {(x+3)/8, -(y+1)/5, (z+10)/14}](/files/3D-LinesLine2pts1.png)
Line 1 pt, 1 vector
Find Cartesian equation of line given 1 point and 1 direction vector on line.
Input: A, P
- A is point vector on line
- P is direction vector along line
Output: C
- C is list representing Cartesian equation
C = {(x-a)/b, (y-c)/d, (z-e)/f} represents (x-a)/b = (y-c)/d = (z-e)/f
r = A + λP
Example
Find a Cartesian equation of the line \(\mathbf{r}(\lambda) = -\mathbf{i} + \mathbf{j} - 3\mathbf{k} + \lambda(2\mathbf{i} + 4\mathbf{j} - 7\mathbf{k})\).
![A = [-1, 1, -3]; P = [2, 4, -7]](/files/3D-LinesLine1pt1vector0.png)
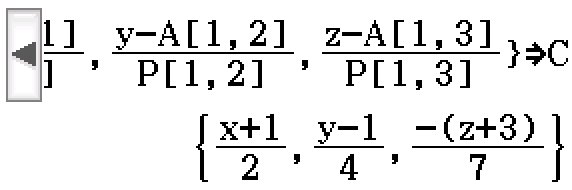
Line Cartesian
Find vector equation of line given Cartesian equation of line.
Input: C
- C is list representing Cartesian equation
Output: A, P
- A is point vector on line
- P is direction vector along line
C = {(x-a)/b, (y-c)/d, (z-e)/f} represents (x-a)/b = (y-c)/d = (z-e)/f
r = A + λP
Example
Find a vector equation of the line \(\dfrac{x+3}{2} = \dfrac{2-y}{3} = \dfrac{z+1}{5}\).
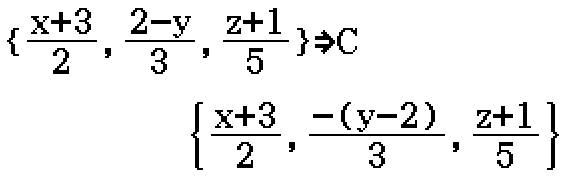
![A = [-3, 2, -1]; P = [2, -3, 5]](/files/3D-LinesLineCartesian1.png)
Distance point-line
Find shortest distance between point and line.
Input: P, A, B
- P is point vector of point
- A is point vector on line
- B is direction vector along line
Output: D, M
- D is shortest distance
- M is point vector on line closest to P
r = A + λB
Example
\(A = (1, 1, 2)\), \(B = (1, 2, 3)\) and \(C = (3, 2, 4)\). Find the shortest distance from \(B\) to line segment \(AC\). (2023 Specialist Exam 2 Section B Question 5b)
![P = [1, 2, 3]; A = [1, 1, 2]; B = [3, 2, 4] - [1, 1, 2]](/files/3D-LinesDistancepointline0.png)
![D = 1; M = [5/3, 4/3, 8/3]](/files/3D-LinesDistancepointline1.png)
Distance line-line
Find shortest distance between two lines.
Input: rA, vA, rB, vB
- rA is point vector on line A
- vA is direction vector along line A
- rB is point vector on line B
- rB is direction vector along line B
Output: AB, D
- AB is shortest vector between lines (perpendicular to both lines)
- D is shortest distance
r = rA + λvA
r = rB + μvB
Example
Find the shortest distance between the lines \(\mathbf{r}(t) = 4\mathbf{i} + 2\mathbf{j} + \mathbf{k} + t(-\mathbf{i} + \mathbf{j} + 3\mathbf{k})\) and \(\mathbf{r}(s) = 5\mathbf{i} + 4\mathbf{j} - 2\mathbf{k} + s(-\mathbf{i} + \mathbf{j} + 3\mathbf{k})\). (Sample Specialist Exam 2 Section B Question 4a)
![rA = [4, 2, 1]; vA = [-1, 1, 3]; rB = [5, 4, -2]; vB = [-1, 1, 3]](/files/3D-LinesDistancelineline0.png)
![AB = [(11mu-8)/11-mu+1, -(11mu-8)/11+mu+2, -3(11mu-8)/11+3mu-3]; D = 3 sqrt(110) / 11](/files/3D-LinesDistancelineline1.png)
Intersection line-line
Find intersection between two lines.
Input: rA, vA, rB, vB
- rA is point vector on line A
- vA is direction vector along line A
- rB is point vector on line B
- vB is direction vector along line B
Output: Soln1, Soln2, X
- Check Soln1 and Soln2 are the same. If different, then lines do not intersect.
- X is point vector of intersection
r = rA + λvA
r = rB + μvB
Example
Find \(a\) and the point of intersection between the intersecting lines \(\mathbf{r}(t) = \mathbf{i} - 3\mathbf{j} + 6\mathbf{k} + t(3\mathbf{i} + 5\mathbf{j} - a\mathbf{k})\) and \(\mathbf{r}(s) = -6\mathbf{i} + 2\mathbf{j} + \mathbf{k} + s(4\mathbf{i} - 10\mathbf{j} + 6\mathbf{k})\). (Sample Specialist Exam 2 Section B Question 4b)
![rA = [1, -3, 6]; vA = [3, 5, -a]; rB = [-6, 2, 1]; vB = [4, -10, 6]](/files/3D-LinesIntersectionlineline0.png)
![Soln1 = {lambda=-1, mu=1}; Soln2 = {lambda=-11/(2a+9), mu=(7a+15)/(4a+18); X = [-2, -8, a+6]](/files/3D-LinesIntersectionlineline1.png)
Angle line-line
Find both angles between two lines.
Input: vA, vB
- vA is direction vector along line A
- vB is direction vector along line B
Output: θ1, θ2
- θ1, θ2 are angles
r = rA + λvA
r = rB + μvB
Example
Find the angles between the lines \(\mathbf{r}(t) = \mathbf{i} + 2\mathbf{k} + t(2\mathbf{i} - \mathbf{j} + \mathbf{k})\) and \(\mathbf{r}(s) = -2\mathbf{i} + 2\mathbf{j} + \mathbf{k} + s(-3\mathbf{i} + 2\mathbf{j} - \mathbf{k})\).
![vA = [2, -1, 1]; vB = [-3, 2, -1]](/files/3D-LinesAnglelineline0.png)
