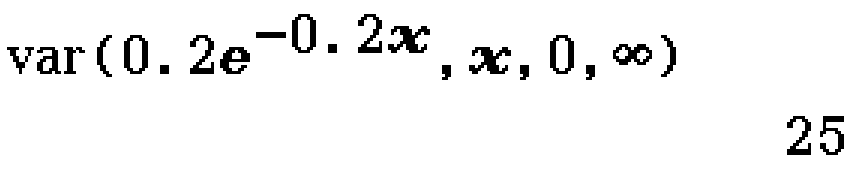aroc (Function)
Command last updated 4/7/2022.
aroc(f, x, a, b)
- f is an expression in terms of x
- x is a variable name
- a is the x-value of the starting point
- b is the x-value of the ending point
Returns the average rate of change of f between x=a and x=b.
Example
Find the average rate of change of \(h(t) = -60 \cos \left( \dfrac{\pi t}{15} \right) + 75\), between \(t=0\) and \(t=\dfrac{30}{4}\). (2023 Methods Exam 2 Section B Question 2c)
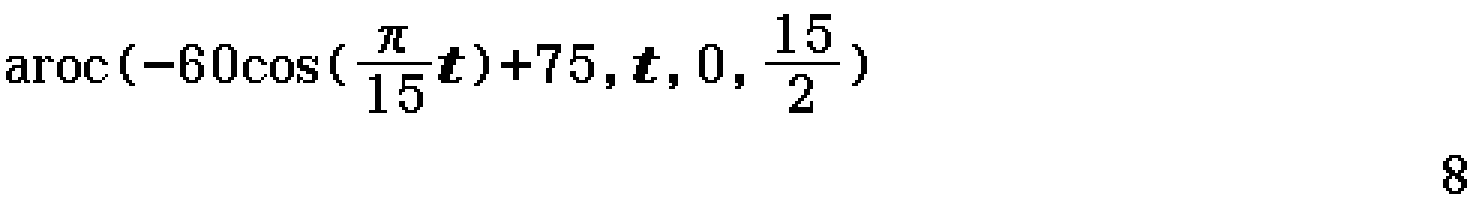
Contributed by Nhan
avalue (Function)
Command last updated 4/7/2022.
avalue(f, x, a, b)
- f is an expression in terms of x
- x is a variable name
- a is the x-value of the starting point
- b is the x-value of the ending point
Returns the average value of f between x=a and x=b.
Example
Find the average value of \(h(t) = -60 \cos \left( \dfrac{\pi t}{15} \right) + 75\), between \(t=0\) and \(t=\dfrac{30}{4}\). (2023 Methods Exam 2 Section B Question 2b)

Contributed by Nhan
axisints (Program)
Command last updated 9/7/2022.
IMPORTANT - requires printpts stored in the same folder as your current folder or in the “library” folder (see the Variable Manager).
axisints(f, l, u)
- f is an expression in terms of x
- l is the lower boundary of x (l should not be in terms of unknown variables, and should be -∞ if f contains other unknown variables besides x)
- u is the upper boundary of x (u should not be in terms of unknown variables, and should be ∞ if f contains other unknown variables besides x)
Returns a list of coordinates of x-axis and y-axis intercepts on f in the domain xϵ[l, u].
Example
Find the axis intercepts of \(y = x(x - 2)(x + 1)\). (2023 Methods Exam 2 Section B Question 1a)
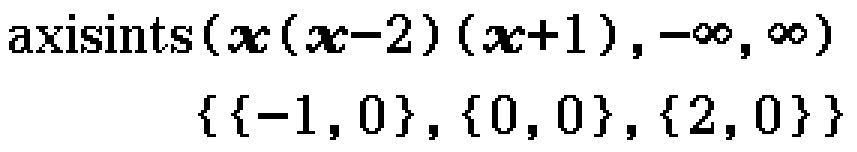
Contributed by Nhan
biCDf (Function)
Command last updated 4/7/2022.
biCDf(l, u, n, p)
- l is the query lower boundary
- u is the query upper boundary
- n is the number of trials
- p is the probability of success each trial
l and u should evaluate to numbers, not expressions in terms of unknown variables. Prefer to use discrete if it would be more appropriate.
Equivalent to the builtin binomialCDf(l, u, n, p), but returns exact values in Standard mode whereas binomialCDf can return only decimal answers.
Returns the probability of between and including l and u successes from n trials with p probability of success each trial.
Example
Let \(X \sim \mathrm{Bi}(7, p)\). Find \(\mathrm{Pr}(2 \leq X \leq 3)\) as a polynomial in terms of \(p\). (2017 Methods Exam 2 Section B Question 3f)
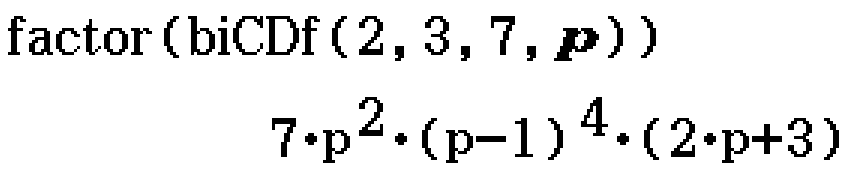
Contributed by Nhan
biPDf (Function)
Command last updated 4/7/2022.
biPDf(x, n, p)
- x is the query integer
- n is the number of trials
- p is the probability of success each trial
Equivalent to the builtin binomialPDf(x, n, p), but returns exact values in Standard mode whereas binomialPDf can return only decimal answers.
Returns the probability of x successes from n trials with p probability of success each trial.
Example
A box contains \(n\) green balls and \(m\) red balls. A ball is selected at random, then replaced in the box. Find the probability that in 8 such selections a green ball is selected at least once. (2023 Methods Exam 2 Section A Question 8)
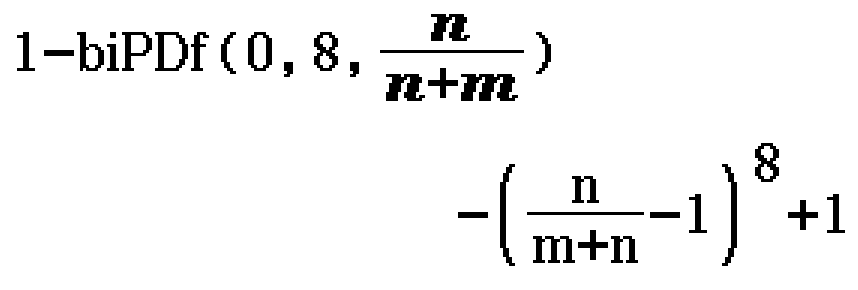
Contributed by Nhan
bmeth (Program)
Command last updated 4/11/2025.
bmeth(f, xl, xh, n)
- f is an expression in terms of x (execution of Program may fail if there are other unknown variables in the expression)
- [xl, xh] is an interval containing a root of f
- n is the number of iterations
Applies the bisection method for n iterations. Returns a matrix with the details of each iteration.
Example
Find the \(x\)-value for a root of \(\sin(x)\) estimated by the bisection method, with an initial range of \([3, 5]\), after 2 iterations.

Contributed by Nhan, Pat
discrete (Function)
Command last updated 4/7/2022.
Note - this program does not work in all cases, such as biCDf (use the builtin binomialCDf instead). Answers should be tested by the user.
discrete(”f ”, x, l, u, h)
- f is an expression in terms of x, enclosed in ” ”
- x is a variable name
- l is the x-value of the starting point
- u is the x-value of the ending point
- h is the step size
Returns a matrix with x-values in the left column and f-values at the corresponding x-values in the right column, for discrete values of x with step size h in the domain [l,u].
Example
\(X \sim \mathrm{Bi}(n, 0.1)\). Find the least \(n\) such that \(\mathrm{Pr}(X \geq 2) \geq 0.5\). (2021 Methods Exam 2 Section A Question 17)

Contributed by Nhan
hCDf (Function)
Command last updated 4/7/2022.
hCDf(l, u, n, M, N)
- l is the query lower boundary
- u is the query upper boundary
- n is the number of draws from the population
- M is the number of successes in the population
- N is the population size
Parameters should evaluate to numbers, not expressions in terms of unknown variables.
Equivalent to the builtin hypergeoCDf(l, u, n, M, N), but returns exact values in Standard mode whereas hypergeoCDf can return only decimal answers.
Returns the probability of between and including l and u successes from n draws, without replacement between draws, from a population size N that contains M successes.
The hypergeometric distribution is not on the VCE Mathematical Methods Study Design, but can be useful for certain examination questions. See the Example. Students are expected to, and should be able to, answer these questions using alternative Mathematical Methods. This function should be used only for checking, and only with an understanding of the circumstances in which the hypergeometric distribution applies.
Example
A bag contains 5 blue marbles and 4 red marbles. 4 balls are taken from the bag, without replacement between draws. Find the probability that the proportion of blue marbles in the 4 draws is greater than half. (2017 NHT Methods Exam 2 Section A Question 11)
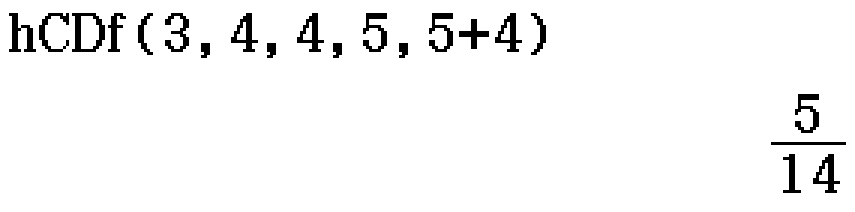
Contributed by Nhan
hPDf (Function)
Command last updated 4/7/2022.
hPDf(x, n, M, N)
- x is the query integer
- n is the number of draws from the population
- M is the number of successes in the population
- N is the population size
Equivalent to the builtin hypergeoPDf(x, n, M, N), but returns exact values in Standard mode whereas hypergeoPDf can return only decimal answers.
Returns the probability of x successes from n draws, without replacement between draws, from a population size N that contains M successes.
The hypergeometric distribution is not on the VCE Mathematical Methods Study Design, but can be useful for certain examination questions. See the Example. Students are expected to, and should be able to, answer these questions using alternative Mathematical Methods. This function should be used only for checking, and only with an understanding of the circumstances in which the hypergeometric distribution applies.
Example
A box contains n marbles, of which k marbles are coloured red and the remainder n-k marbles are coloured green. 2 marbles are drawn from the box, without replacement between draws. Find the probability that the 2 marbles drawn are the same colour. (2019 Methods Exam 2 Section A Question 17)
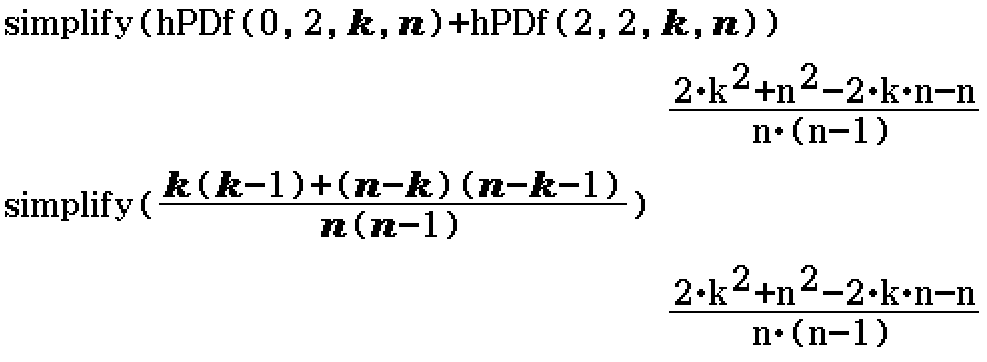
Contributed by Nhan
infpts (Program)
Command last updated 23/11/2022.
IMPORTANT - requires printpts stored in the same folder as your current folder or in the “library” folder (see the Variable Manager).
infpts(f, l, u)
- f is an expression in terms of x
- l is the lower boundary of x (l should not be in terms of unknown variables, and should be -∞ if f contains other unknown variables besides x)
- u is the upper boundary of x (u should not be in terms of unknown variables, and should be ∞ if f contains other unknown variables besides x)
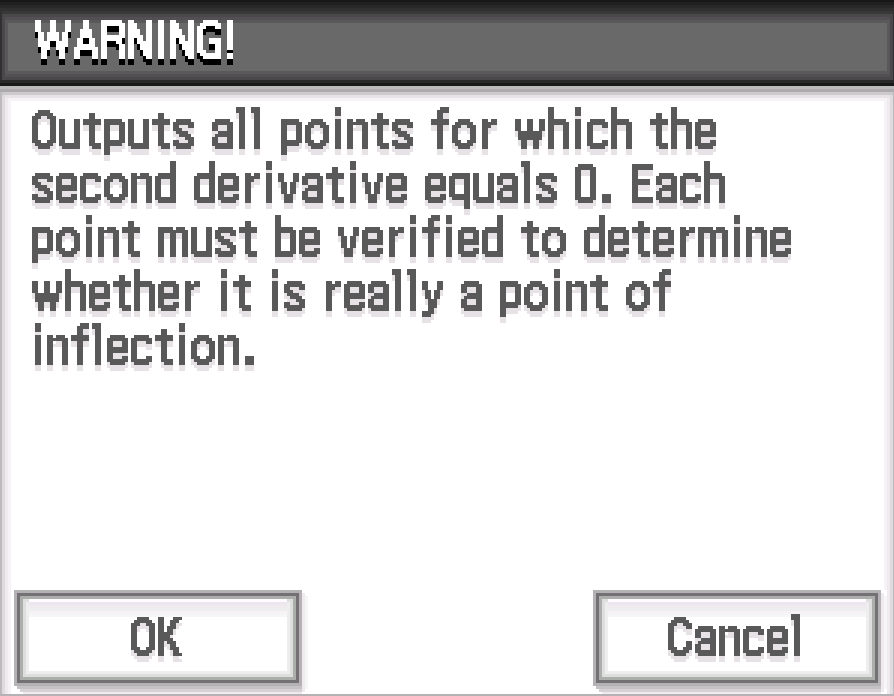
Returns a list of coordinates of points on f in the domain xϵ[l, u] where the second derivative equals 0.
Each point must be verified to determine whether it is really a point of inflection.
Example
Find the coordinates of any points of inflection of the graph of \(\dfrac{x}{1+x^{3}}\). (2017 Specialist Exam 2 Section B Question 1aiii)
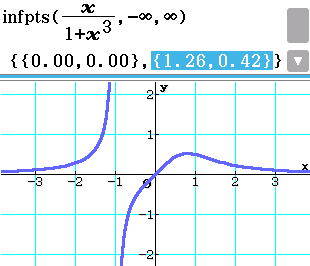
Contributed by Nhan
intpts (Program)
Command last updated 9/7/2022.
IMPORTANT - requires printpts stored in the same folder as your current folder or in the “library” folder (see the Variable Manager).
intpts(f, g, l, u)
- f is an expression in terms of x
- g is an expression in terms of x
- l is the lower boundary of x (l should not be in terms of unknown variables, and should be -∞ if either f or g contains other unknown variables besides x)
- u is the upper boundary of x (u should not be in terms of unknown variables, and should be ∞ if either f or g contains other unknown variables besides x)
Returns a list of coordinates of points of intersection of f and g.
Example
Find the coordinates of the points of intersection of the graphs of \((x-1)^3 (x+2)^3\) and \((x-1)^2 (x+2)^3\). (2019 NHT Methods Exam 2 Section B Question 1a)
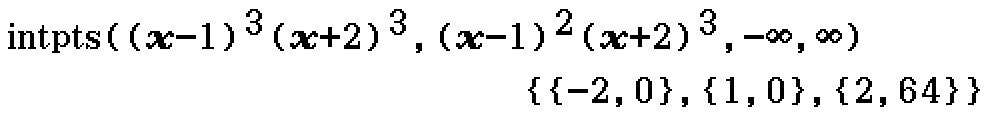
Contributed by Nhan
keypts (Program)
Command last updated 9/7/2022.
IMPORTANT - requires printpts stored in the same folder as your current folder or in the “library” folder (see the Variable Manager).
keypts(f, l, u)
- f is an expression in terms of x (execution of Program may partially fail if there are other unknown variables in the expression)
- l is the lower boundary of x (l should not be in terms of unknown variables)
- u is the upper boundary of x (u should not be in terms of unknown variables)
Prints and categorises coordinates of key points on y=f in the domain xϵ[l, u].
- y-axis intercepts where x=0
- x-axis intercepts where y=0
- stationary points where f \('\)=0
- local minima where f \(''\)>0
- local maxima where f \(''\)<0
- stationary points of inflection where f \(''\)=0 and f \('''\)≠0
- stationary points of unknown nature where f \(''\)=0 and f \('''\)=0 (users should verify the nature of these points themselves)
- points of inflection where f \(''\)=0 and f \('''\)≠0
- possible points of inflection where f \(''\)=0 and f \('''\)=0 (users should verify the nature of these points themselves)
- endpoints where x=l and x=u
The 2nd and 3rd derivative tests are not on the VCE Mathematical Methods Study Design.
Example
Find key points on \(y = \dfrac{1}{5} x^5 + \dfrac{3}{4} x^4 - 2x^2 + \dfrac{12}{5}\) for \(x \in (-\infty, 2]\).
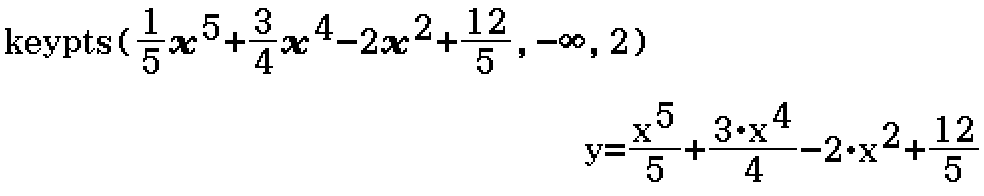



Contributed by Nhan
lineof (Function)
Command last updated 4/7/2022.
lineof(a, b, c, d, x)
- (a, b) are the coordinates of a point
- (c, d) are the coordinates of a point
- x is a variable name
Returns an expression for the line connecting points (a, b) and (c, d) in terms of x.
Example
Let \(f(x) = x^3 - 5x\). Find the equation of the line through \((-1, f(-1))\) and \((1, f(1))\). (2017 Methods Exam 2 Section B Question 1bi)
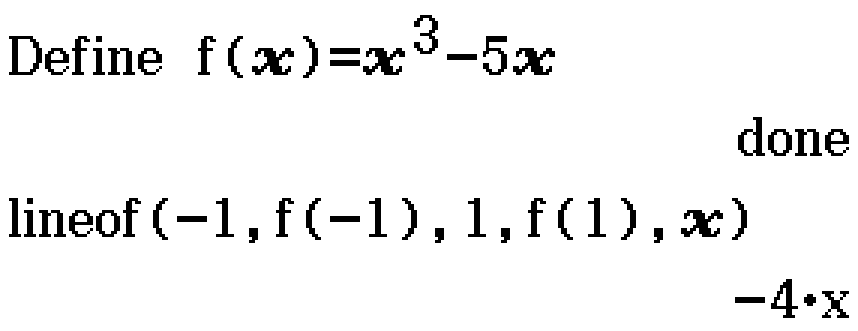
Contributed by Nhan
mu (Function)
Command last updated 4/7/2022.
mu(f, x, a, b)
- f is an expression in terms of x
- x is a variable name
- a is the x-value of the starting point
- b is the x-value of the ending point
For fastest calculation time, the domain [a, b] should be as small as possible.
If f is a piecewise function it should be entered raw not as a user-defined function.
The integral of f over the domain [a, b] must equal 1, as this is assumed by the mu function.
Returns the mean of the continuous probability distribution defined by the probability density function f over the domain [a, b].
Example
Find the expected value of \(v\) for the probability density function
[f(v) =
\left{ \begin{array}{ll}
\dfrac{1}{6 \pi} \sin \left( \sqrt{ \dfrac{v-30}{3} } \right) & 30 \leq v \leq 3 \pi^2 + 30
\ 0 & \mathrm{elsewhere} \end{array}
\right.]
(2023 Methods Exam 2 Section B Question 4i)
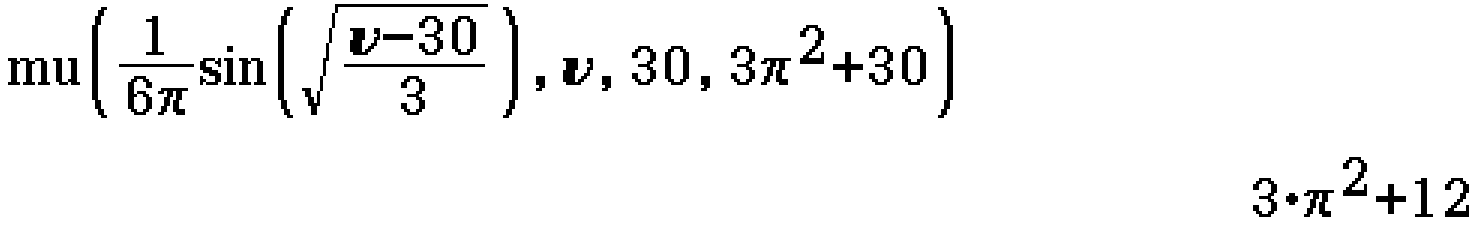
Contributed by Nhan
nPDf (Function)
Command last updated 4/7/2022.
nPDf(x, σ, μ)
- x is a number or variable name
- σ is the standard deviation
- μ is the mean
Equivalent to the builtin normPDf(x, σ, μ), but more convenient to obtain the specific probability density function and to graph the function.
Returns the value of the normal distribution function with a standard deviation of σ and a mean of μ at the value x.
Example
Let \(M \sim \mathrm{N}(68, 8^2)\). Find \(\mathrm{Pr}(60<M<90)\). (2018 Methods Exam 2 Section B Question 4a)
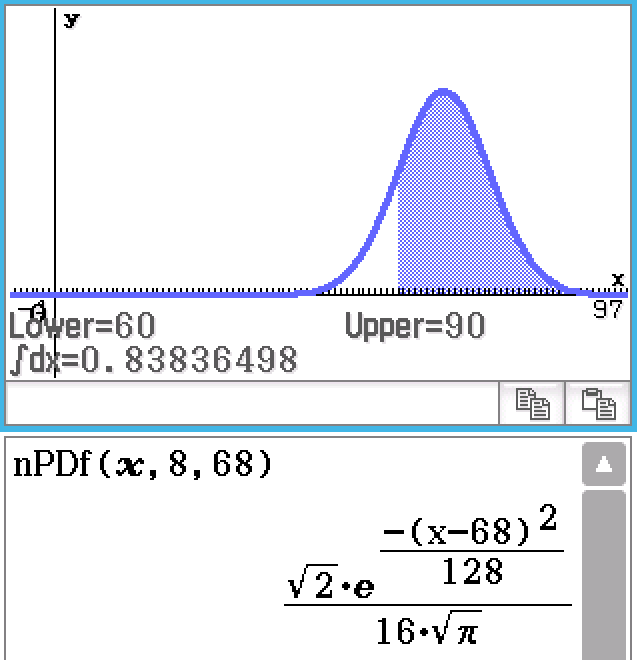
Contributed by Nhan
nmeth (Program)
Command last updated 4/11/2025.
nmeth(f, xa, n)
- f is an expression in terms of x (execution of Program may fail if there are other unknown variables in the expression)
- xa is the initial guess for the x-value of a root of f
- n is the number of iterations
Applies Newton’s method to approximate an x-intercept of f for n iterations. Returns a matrix with the details of each iteration.
Example
Find \(x_1\), \(x_2\) and \(x_3\) using Newton’s method with \(x_0 = 0\) to approximate an x-intercept of \(h(x) = 2^x - x^2\). (2023 Methods Exam 2 Section B Question 3f)

Contributed by Nhan, Pat
pcheck (Program)
Command last updated 6/3/2024.
Note - this program may throw an error if in Decimal mode. Use Standard mode instead.
Define f(x) = {a, b, c, d, e}
pcheck(f(x), l, r)
- f(x) is defined as a list of any length containing expressions {a, b, …} in terms of x
- l is the left hand side of the equation
- r is the right hand side of the equation
Returns a matrix with each row corresponding to an option of f(x), with the columns containing for that option, from left to right, f(x), l, r, judge(l=r).
Example
\(f(x+f(x)) = f(2x)\). Which option could possibly be \(f(x)\)? (2018 Methods Exam 2 Section A Question 10)
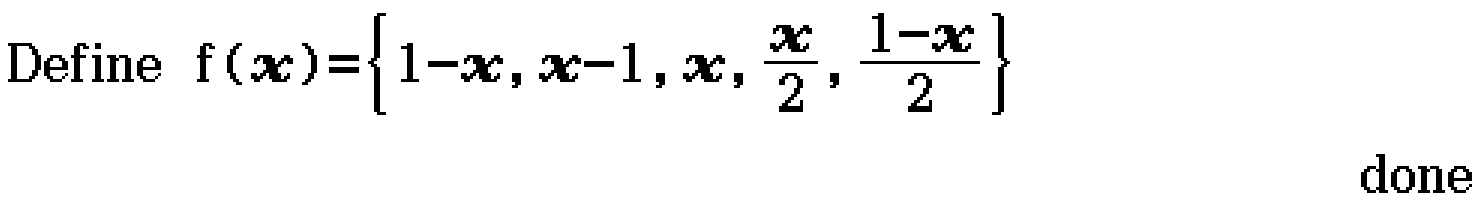
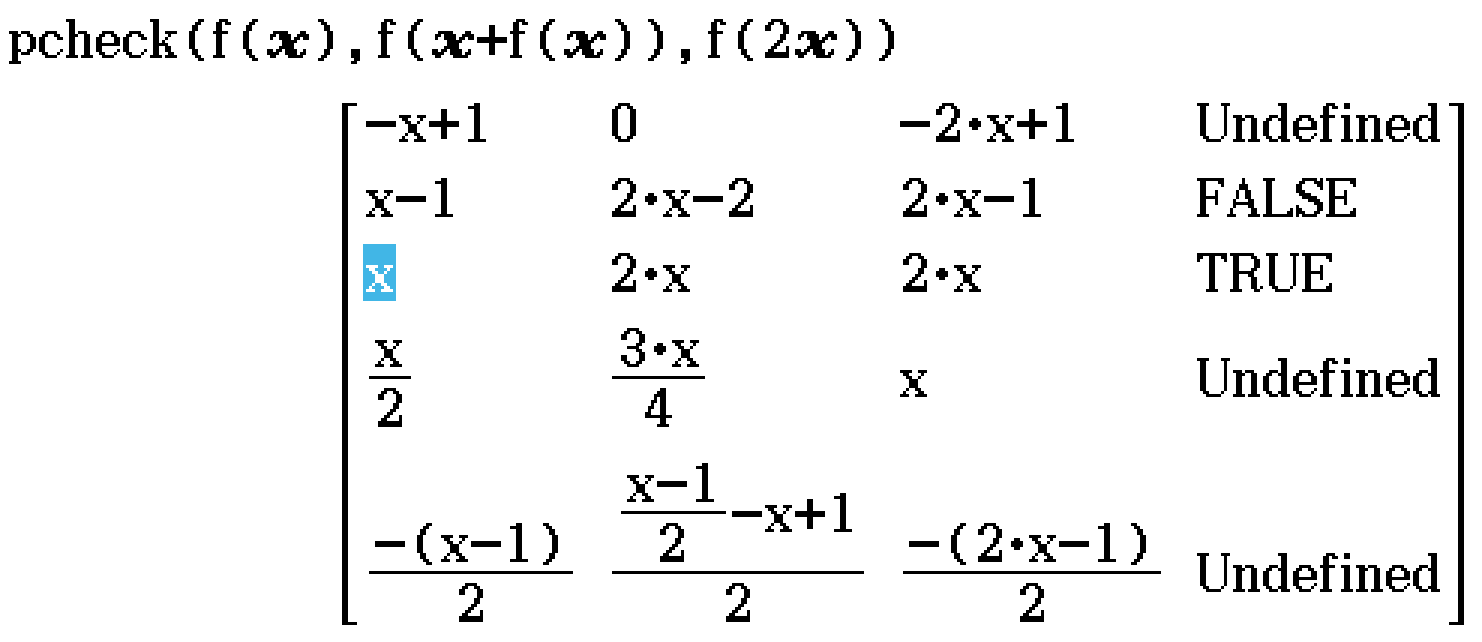
Contributed by Nhan and Kevin
printpts (Program)
Command last updated 9/7/2022.
printpts(f, {s})
- f is an expression in terms of x
- s is a list of x-values, enclosed in { }
Returns a list of coordinates of points on f corresponding to the x-values in s.
Example
Find the \(y\)-values of the points where \(x = - \infty, -1, 0, 1, \infty\) on \(y = (x-1)^2 (x+2)^3\).
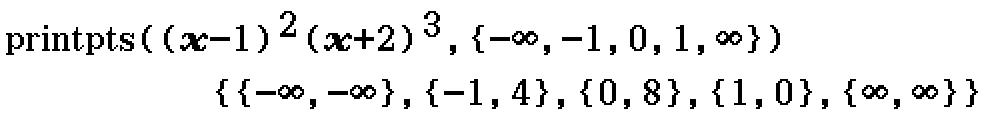
Contributed by Nhan
sd (Function)
Command last updated 4/7/2022.
sd(f, x, a, b)
- f is an expression in terms of x
- x is a variable name
- a is the x-value of the starting point
- b is the x-value of the ending point
For fastest calculation time, the domain [a, b] should be as small as possible.
If f is a piecewise function it should be entered raw not as a user-defined function.
The integral of f over the domain [a, b] must equal 1, as this is assumed by the sd function.
Returns the standard deviation of the continuous probability distribution defined by the probability density function f over the domain [a, b].
Example
Find the standard devation of \(x\) for the probability density function
[\left{ \begin{array}{ll}
\dfrac{x}{500} & 0 \leq x < 20
\dfrac{50-x}{750} & 20 \leq x \leq 50
\ 0 & \text{elsewhere} \end{array}
\right.]
(2021 Methods Exam 2 Section B Question 4g)
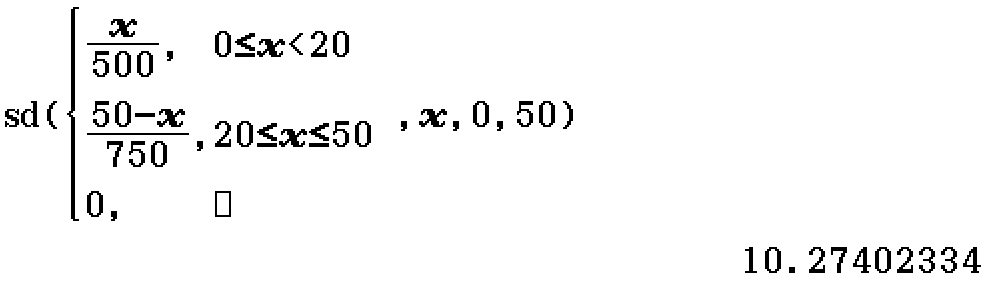
Contributed by Nhan
simlin (Function)
Command last updated 4/7/2022.
simlin(a, b, c, d, e, f, g)
- a, b, c are numbers or expressions in terms of g, representing a line ax+by=c
- d, e, f are numbers or expressions in terms of g, representing a line dx+ey=f
- g is a variable name
Returns a list.
- 1st item is values of g for which the 2 lines intersect 0 times.
- 2nd item is values of g for which the 2 lines intersect 1 time.
- 3rd item is values of g for which the 2 lines intersect ∞ times.
Example
Find the largest set of values of \(k\) for which the simultaneous linear equations \(kx+5y=k+5\) and \(4x+(k+1)y=0\) have ∞ solutions for \((x, y)\). (2023 Methods Exam 2 Section A Question 4)
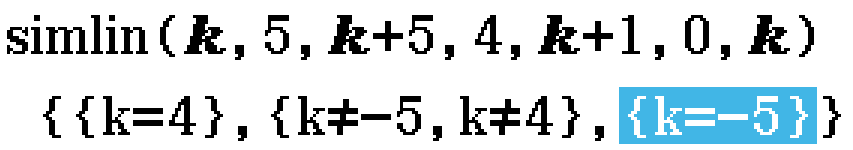
Contributed by Nhan
statpts (Program)
Command last updated 9/7/2022.
IMPORTANT - requires printpts stored in the same folder as your current folder or in the “library” folder (see the Variable Manager).
statpts(f, l, u)
- f is an expression in terms of x
- l is the lower boundary of x (l should not be in terms of unknown variables, and should be -∞ if f contains other unknown variables besides x)
- u is the upper boundary of x (u should not be in terms of unknown variables, and should be ∞ if f contains other unknown variables besides x)
Returns a list of coordinates of stationary points on f in the domain xϵ[l, u].
Example
Find the coordinates of the stationary points of \(f(x) = x(x-2)(x+1)\). (2023 Methods Exam 2 Section B Question 1b)

Contributed by Nhan
trans (Function)
Command last updated 6/3/2024.
trans(e, t, x, y)
- e is an equation in terms of x and y
- t is a matrix transformation of x and y
- x and y are variable names
Returns the equation after the transformation is applied.
Example
\(f(x) = e^x + e^{-x}\) and \(g(x) = \dfrac{1}{2} f(2-x)\). Find a possible sequence of transformations that map \(f\) to \(g\). (2023 Methods Exam 2 Section B Question 5a)
![trans(y=f(x), [[-1 0] [0 1/2]][[x] [y]] + [[2] [0]], x, y)](/files/trans0.png)

Contributed by Nhan
trsum (Function)
Command last updated 21/7/2022.
trsum(f, v, a, b, w)
- f is an expression in terms of v
- v is a variable name
- a is the v-value of the starting point
- b is the v-value of the ending point
- w is the trapezium width
Returns the approximation to \(\int_a^b f dv\) using trapeziums of width w and vertical parallel side lengths equal to the value of f at the trapezium’s left and right endpoints.
Example
Find the approximation of
[\int_0^{4} \left( \dfrac{1}{27} (x-3)^2 (x+3)^2 + 1 \right) dx]
using the trapezium rule with trapeziums of width \(1\). (Sample Methods Exam 2 Section A Question 3)

Contributed by Nathan Chen
var (Function)
Command last updated 4/7/2022.
var(f, x, a, b)
- f is an expression in terms of x
- x is a variable name
- a is the x-value of the starting point
- b is the x-value of the ending point
For fastest calculation time, the domain [a, b] should be as small as possible.
If f is a piecewise function it should be entered raw not as a user-defined function.
The integral of f over the domain [a, b] must equal 1, as this is assumed by the var function.
Returns the variance of the continuous probability distribution defined by the probability density function f over the domain [a, b].
Example
Find the expected value of \(x\) for the probability density function
[\left{ \begin{array}{ll}
0.2e^{-0.2x} & x \geq 0
\ 0 & x < 0 \end{array}
\right.]
(2021 NHT Methods Exam 2 Section A Question 14)